Alpha Selection

Regularization is designed to penalize model complexity, therefore the higher the alpha, the less complex the model, decreasing the error due to variance (overfit). Alphas that are too high on the other hand increase the error due to bias (underfit). It is important, therefore to choose an optimal alpha such that the error is minimized in both directions.

The AlphaSelection Visualizer demonstrates how different values of alpha influence model selection during the regularization of linear models. Generally speaking, alpha increases the affect of regularization, e.g. if alpha is zero there is no regularization and the higher the alpha, the more the regularization parameter influences the final model.

Visualizer	AlphaSelection
Quick Method	alphas()
Models	Regression
Workflow	Model selection, Hyperparameter tuning

For Estimators with Built-in Cross-Validation

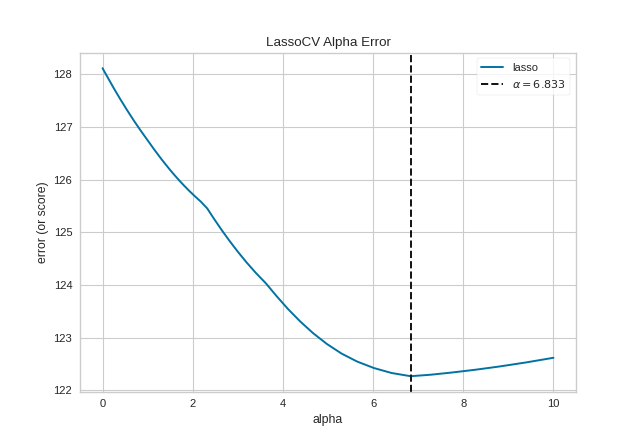
The AlphaSelection visualizer wraps a “RegressionCV” model and visualizes the alpha/error curve. Use this visualization to detect if the model is responding to regularization, e.g. as you increase or decrease alpha, the model responds and error is decreased. If the visualization shows a jagged or random plot, then potentially the model is not sensitive to that type of regularization and another is required (e.g. L1 or Lasso regularization).

Note

The AlphaSelection visualizer requires a “RegressorCV” model, e.g. a specialized class that performs cross-validated alpha-selection on behalf of the model. See the ManualAlphaSelection visualizer if your regression model does not include cross-validation.

import numpy as np

from sklearn.linear_model import LassoCV
from yellowbrick.datasets import load_concrete
from yellowbrick.regressor import AlphaSelection

# Load the regression dataset
X, y = load_concrete()

# Create a list of alphas to cross-validate against
alphas = np.logspace(-10, 1, 400)

# Instantiate the linear model and visualizer
model = LassoCV(alphas=alphas)
visualizer = AlphaSelection(model)
visualizer.fit(X, y)
visualizer.show()

(Source code, png, pdf)

For Estimators without Built-in Cross-Validation

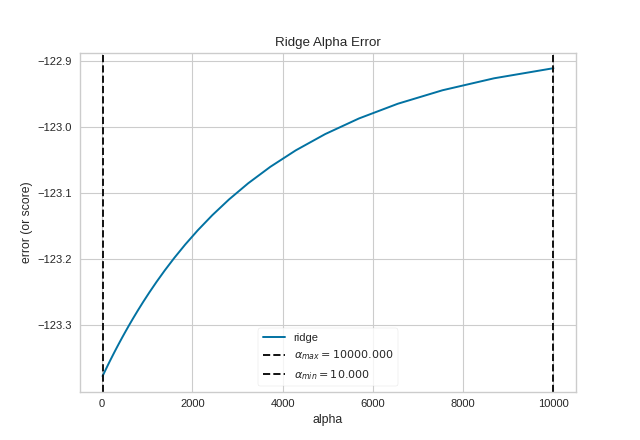
Most scikit-learn Estimators with alpha parameters have a version with built-in cross-validation. However, if the regressor you wish to use doesn’t have an associated “CV” estimator, or for some reason you would like to specify more control over the alpha selection process, then you can use the ManualAlphaSelection visualizer. This visualizer is essentially a wrapper for scikit-learn’s cross_val_score method, fitting a model for each alpha specified.

import numpy as np

from sklearn.linear_model import Ridge
from yellowbrick.datasets import load_concrete
from yellowbrick.regressor import ManualAlphaSelection

# Load the regression dataset
X, y = load_concrete()

# Create a list of alphas to cross-validate against
alphas = np.logspace(1, 4, 50)

# Instantiate the visualizer
visualizer = ManualAlphaSelection(
    Ridge(),
    alphas=alphas,
    cv=12,
    scoring="neg_mean_squared_error"
)

visualizer.fit(X, y)
visualizer.show()

(Source code, png, pdf)

Quick Methods

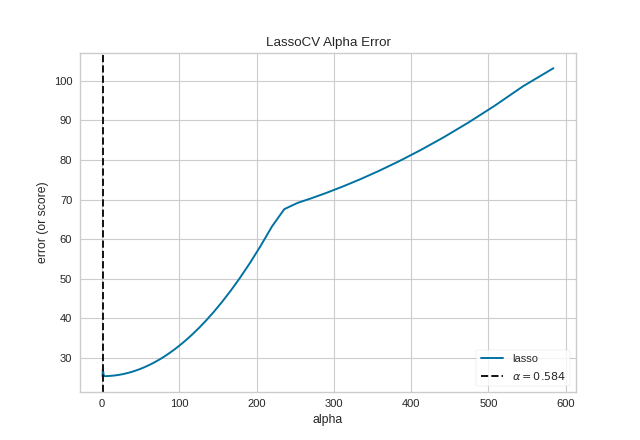
The same functionality above can be achieved with the associated quick method alphas. This method will build the AlphaSelection Visualizer object with the associated arguments, fit it, then (optionally) immediately show it.

from sklearn.linear_model import LassoCV
from yellowbrick.regressor.alphas import alphas

from yellowbrick.datasets import load_energy

# Load dataset
X, y = load_energy()

# Use the quick method and immediately show the figure
alphas(LassoCV(random_state=0), X, y)

(Source code, png, pdf)

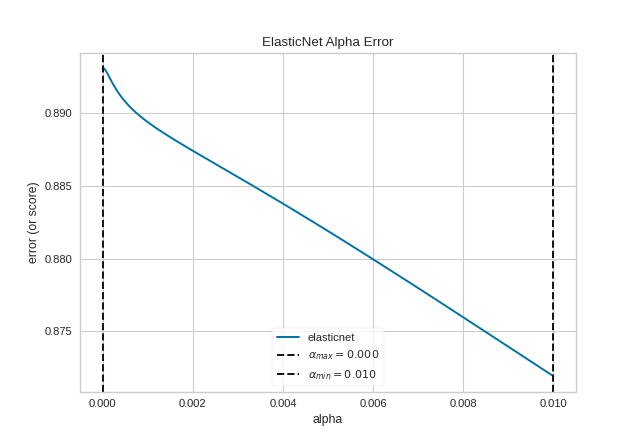
The ManualAlphaSelection visualizer can also be used as a oneliner:

from sklearn.linear_model import ElasticNet
from yellowbrick.regressor.alphas import manual_alphas

from yellowbrick.datasets import load_energy

# Load dataset
X, y = load_energy()

# Instantiate a model
model = ElasticNet(tol=0.01, max_iter=10000)

# Use the quick method and immediately show the figure
manual_alphas(model, X, y, cv=6)

(Source code, png, pdf)

API Reference

Implements alpha selection visualizers for regularization

class yellowbrick.regressor.alphas.AlphaSelection(estimator, ax=None, is_fitted='auto', **kwargs)

Bases: RegressionScoreVisualizer

The Alpha Selection Visualizer demonstrates how different values of alpha influence model selection during the regularization of linear models. Generally speaking, alpha increases the affect of regularization, e.g. if alpha is zero there is no regularization and the higher the alpha, the more the regularization parameter influences the final model.

Regularization is designed to penalize model complexity, therefore the higher the alpha, the less complex the model, decreasing the error due to variance (overfit). Alphas that are too high on the other hand increase the error due to bias (underfit). It is important, therefore to choose an optimal Alpha such that the error is minimized in both directions.

To do this, typically you would you use one of the “RegressionCV” models in Scikit-Learn. E.g. instead of using the Ridge (L2) regularizer, you can use RidgeCV and pass a list of alphas, which will be selected based on the cross-validation score of each alpha. This visualizer wraps a “RegressionCV” model and visualizes the alpha/error curve. Use this visualization to detect if the model is responding to regularization, e.g. as you increase or decrease alpha, the model responds and error is decreased. If the visualization shows a jagged or random plot, then potentially the model is not sensitive to that type of regularization and another is required (e.g. L1 or Lasso regularization).

Parameters

estimatora Scikit-Learn regressor

Should be an instance of a regressor, and specifically one whose name ends with “CV” otherwise a will raise a YellowbrickTypeError exception on instantiation. To use non-CV regressors see: ManualAlphaSelection. If the estimator is not fitted, it is fit when the visualizer is fitted, unless otherwise specified by is_fitted.

axmatplotlib Axes, default: None

The axes to plot the figure on. If None is passed in the current axes will be used (or generated if required).

is_fittedbool or str, default=’auto’

Specify if the wrapped estimator is already fitted. If False, the estimator will be fit when the visualizer is fit, otherwise, the estimator will not be modified. If ‘auto’ (default), a helper method will check if the estimator is fitted before fitting it again.

kwargsdict

Keyword arguments that are passed to the base class and may influence the visualization as defined in other Visualizers.

Notes

This class expects an estimator whose name ends with “CV”. If you wish to use some other estimator, please see the ManualAlphaSelection Visualizer for manually iterating through all alphas and selecting the best one.

This Visualizer hooks into the Scikit-Learn API during fit(). In order to pass a fitted model to the Visualizer, call the draw() method directly after instantiating the visualizer with the fitted model.

Note, each “RegressorCV” module has many different methods for storing alphas and error. This visualizer attempts to get them all and is known to work for RidgeCV, LassoCV, LassoLarsCV, and ElasticNetCV. If your favorite regularization method doesn’t work, please submit a bug report.

For RidgeCV, make sure store_cv_values=True.

Examples

>>> from yellowbrick.regressor import AlphaSelection
>>> from sklearn.linear_model import LassoCV
>>> model = AlphaSelection(LassoCV())
>>> model.fit(X, y)
>>> model.show()

draw()

Draws the alpha plot based on the values on the estimator.

finalize()

Prepare the figure for rendering by setting the title as well as the X and Y axis labels and adding the legend.

fit(X, y, **kwargs)

A simple pass-through method; calls fit on the estimator and then draws the alpha-error plot.

class yellowbrick.regressor.alphas.ManualAlphaSelection(estimator, ax=None, alphas=None, cv=None, scoring=None, **kwargs)

Bases: AlphaSelection

The AlphaSelection visualizer requires a “RegressorCV”, that is a specialized class that performs cross-validated alpha-selection on behalf of the model. If the regressor you wish to use doesn’t have an associated “CV” estimator, or for some reason you would like to specify more control over the alpha selection process, then you can use this manual alpha selection visualizer, which is essentially a wrapper for cross_val_score, fitting a model for each alpha specified.

Parameters

estimatoran unfitted Scikit-Learn regressor

Should be an instance of an unfitted regressor, and specifically one whose name doesn’t end with “CV”. The regressor must support a call to set_params(alpha=alpha) and be fit multiple times. If the regressor name ends with “CV” a YellowbrickValueError is raised.

axmatplotlib Axes, default: None

The axes to plot the figure on. If None is passed in the current axes will be used (or generated if required).

alphasndarray or Series, default: np.logspace(-10, 2, 200)

An array of alphas to fit each model with

cvint, cross-validation generator or an iterable, optional

Determines the cross-validation splitting strategy. Possible inputs for cv are:

• None, to use the default 3-fold cross validation,

• integer, to specify the number of folds in a (Stratified)KFold,

• An object to be used as a cross-validation generator.

• An iterable yielding train, test splits.

This argument is passed to the sklearn.model_selection.cross_val_score method to produce the cross validated score for each alpha.

scoringstring, callable or None, optional, default: None

A string (see model evaluation documentation) or a scorer callable object / function with signature scorer(estimator, X, y).

This argument is passed to the sklearn.model_selection.cross_val_score method to produce the cross validated score for each alpha.

kwargsdict

Keyword arguments that are passed to the base class and may influence the visualization as defined in other Visualizers.

Notes

This class does not take advantage of estimator-specific searching and is therefore less optimal and more time consuming than the regular “RegressorCV” estimators.

Examples

>>> from yellowbrick.regressor import ManualAlphaSelection
>>> from sklearn.linear_model import Ridge
>>> model = ManualAlphaSelection(
...     Ridge(), cv=12, scoring='neg_mean_squared_error'
... )
...
>>> model.fit(X, y)
>>> model.show()

draw()

Draws the alphas values against their associated error in a similar fashion to the AlphaSelection visualizer.

fit(X, y, **args)

The fit method is the primary entry point for the manual alpha selection visualizer. It sets the alpha param for each alpha in the alphas list on the wrapped estimator, then scores the model using the passed in X and y data set. Those scores are then aggregated and drawn using matplotlib.

yellowbrick.regressor.alphas.alphas(estimator, X, y=None, ax=None, is_fitted='auto', show=True, **kwargs)

Quick Method: The Alpha Selection Visualizer demonstrates how different values of alpha influence model selection during the regularization of linear models. Generally speaking, alpha increases the affect of regularization, e.g. if alpha is zero there is no regularization and the higher the alpha, the more the regularization parameter influences the final model.

Parameters

estimatora Scikit-Learn regressor

Should be an instance of a regressor, and specifically one whose name ends with “CV” otherwise a will raise a YellowbrickTypeError exception on instantiation. To use non-CV regressors see: ManualAlphaSelection. If the estimator is not fitted, it is fit when the visualizer is fitted, unless otherwise specified by is_fitted.

Xndarray or DataFrame of shape n x m

A matrix of n instances with m features.

yndarray or Series of length n

An array or series of target values.

axmatplotlib Axes, default: None

The axes to plot the figure on. If None is passed in the current axes will be used (or generated if required).

is_fittedbool or str, default=’auto’

Specify if the wrapped estimator is already fitted. If False, the estimator will be fit when the visualizer is fit, otherwise, the estimator will not be modified. If ‘auto’ (default), a helper method will check if the estimator is fitted before fitting it again.

showbool, default: True

If True, calls show(), which in turn calls plt.show() however you cannot call plt.savefig from this signature, nor clear_figure. If False, simply calls finalize()

kwargsdict

Keyword arguments that are passed to the base class and may influence the visualization as defined in other Visualizers.

Returns

visualizerAlphaSelection

Returns the alpha selection visualizer

yellowbrick.regressor.alphas.manual_alphas(estimator, X, y=None, ax=None, alphas=None, cv=None, scoring=None, show=True, **kwargs)

Quick Method: The Manual Alpha Selection Visualizer demonstrates how different values of alpha influence model selection during the regularization of linear models. Generally speaking, alpha increases the affect of regularization, e.g. if alpha is zero there is no regularization and the higher the alpha, the more the regularization parameter influences the final model.

Parameters

estimatoran unfitted Scikit-Learn regressor

Should be an instance of an unfitted regressor, and specifically one whose name doesn’t end with “CV”. The regressor must support a call to set_params(alpha=alpha) and be fit multiple times. If the regressor name ends with “CV” a YellowbrickValueError is raised.

axmatplotlib Axes, default: None

The axes to plot the figure on. If None is passed in the current axes will be used (or generated if required).

alphasndarray or Series, default: np.logspace(-10, 2, 200)

An array of alphas to fit each model with

cvint, cross-validation generator or an iterable, optional

Determines the cross-validation splitting strategy. Possible inputs for cv are:

• None, to use the default 3-fold cross validation,

• integer, to specify the number of folds in a (Stratified)KFold,

• An object to be used as a cross-validation generator.

• An iterable yielding train, test splits.

This argument is passed to the sklearn.model_selection.cross_val_score method to produce the cross validated score for each alpha.

scoringstring, callable or None, optional, default: None

A string (see model evaluation documentation) or a scorer callable object / function with signature scorer(estimator, X, y).

This argument is passed to the sklearn.model_selection.cross_val_score method to produce the cross validated score for each alpha.

kwargsdict

Keyword arguments that are passed to the base class and may influence the visualization as defined in other Visualizers.

Returns

visualizerAlphaSelection

Returns the alpha selection visualizer